- SPITZE
- Grundlagen der CAE
- Teil 12: Topologieoptimierung für Design
Serie: Grundlagen der CAE-Analyse für das Kunststoffproduktdesign
Teil 12 Topologieoptimierung für Design
Topologieoptimierung ist eine innovative Technologie, die den Designprozess beschleunigt, Abfall eliminiert und optimale Formen ableitet. Diese Topologieoptimierung stellt die grundlegenden Konzepte und Methoden der Topologieoptimierung für diejenigen vor, die sie noch nicht verwendet haben.
2025.05.07

Inhalt
Einführung
Für viele Designer ist es eine große Herausforderung, die Funktionalität und Leistung eines Produkts zu verbessern und gleichzeitig Kosten- und Fertigungsanforderungen zu erfüllen. Strukturoptimale Lösungen sind eine Methode zur Lösung dieses Problems.
Das Konzept der optimalen Gestaltung von Strukturen gibt es angeblich seit den 1980er Jahren, und nachdem die grundlegenden Theorien in akademischen Kreisen untersucht worden waren, wurde es in der Industrie angewendet, die Rechenleistung von Computern verbesserte sich und in den letzten Jahren wird es in vielen verschiedenen Industriebereichen eingesetzt.
Methoden der Strukturoptimierung
Es gibt drei Hauptmethoden zur Optimierung einer Struktur: Größenoptimierung, Formoptimierung und Topologieoptimierung.
Bei der Dimensionsoptimierung handelt es sich um eine Technik zur Ermittlung optimaler Abmessungen, bei der beliebige Abmessungen, beispielsweise die Länge und Dicke einer Komponente, als Variablen verwendet werden, wie in Abb. 1(a) dargestellt.
Bei der Formoptimierung handelt es sich um eine Technik zur Optimierung der Form eines Teils unter Verwendung der äußeren Form als Variable, wie in Abb. 1(b) dargestellt.
Diese Techniken eignen sich, wenn die äußere Form optimiert werden soll, ohne die Grundstruktur zu verändern. Allerdings können diese Techniken die Strukturform nicht wesentlich verändern, sodass die Struktur möglicherweise nicht optimal ist. Daher ist die Topologieoptimierung, dargestellt in Abb. 1(c), eine Technik, die eine Optimierung mit einem höheren Freiheitsgrad ermöglicht.
In diesem Artikel möchte ich die Topologieoptimierung vorstellen, eine Art strukturelles Optimum.
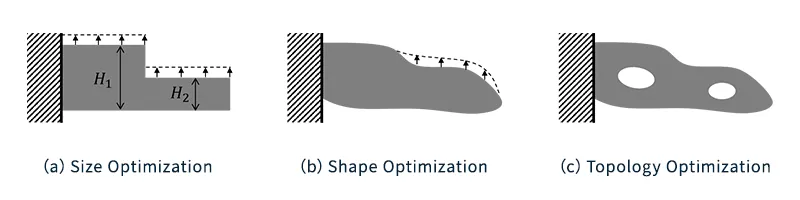 Abb. 1 Strukturoptimale Methode
Abb. 1 Strukturoptimale Methode
Merkmale
Bei der Topologieoptimierung handelt es sich um eine Methode zur Optimierung der Struktur, bei der berechnet wird, wie Materialien im zu gestaltenden Raum angeordnet werden müssen, um eine optimale Struktur zu schaffen.
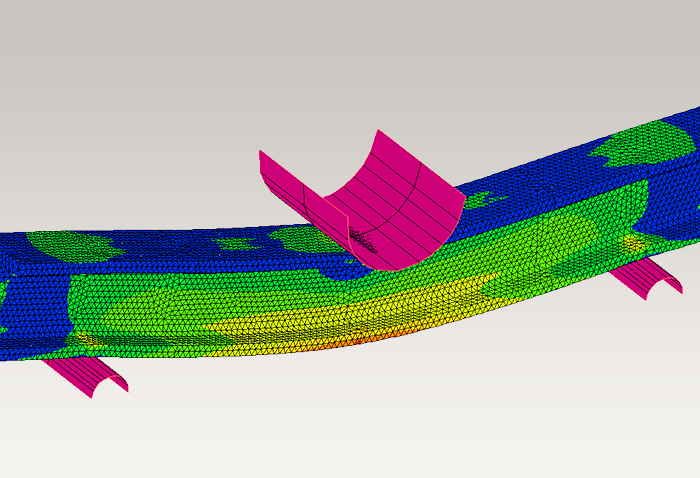
Betrachten wir beispielsweise den Fall, in dem beide Enden gestützt werden und eine Last auf die Unterseite ausgeübt wird, wie links in Abb. 2 gezeigt. Bei der Topologieoptimierung wird der Bereich, in dem Materialien platziert werden können (der sogenannte Designraum, also der optimale Bereich), in kleine Elemente unterteilt und es werden Optimalberechnungen durchgeführt, während die Materialdichte für jedes Element angepasst wird.
Ein Beispiel für die Analyseergebnisse nach der Topologieoptimierung ist rechts in Abb. 2 dargestellt. Die Farbe stellt die Materialdichte dar und durch Platzierung von Material in den rot dargestellten Bereichen mit hoher Dichteverteilung ist es möglich, eine Struktur zu erstellen, die die Festigkeit effizienter gewährleistet.
Die Topologieoptimierung ermöglicht eine Formoptimierung mit einem so hohen Freiheitsgrad, dass sie den großen Vorteil bietet, optimale Lösungen ableiten zu können, die allein mit menschlicher Intuition nur schwer zu erreichen wären.
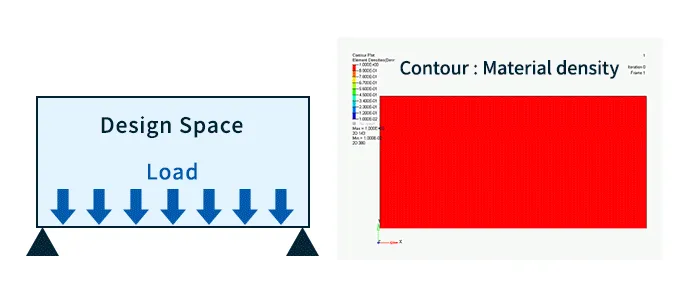 Abb. 2 Ergebnisse der Topologieoptimierung (Kontur : Materialdichte)
Abb. 2 Ergebnisse der Topologieoptimierung (Kontur : Materialdichte)
Für die Topologieoptimierung erforderliche Informationen
Für die Topologieoptimierung sind folgende Informationen erforderlich:
- Designraum
- Verschiedene Eingabedaten (physikalische Eigenschaften, Lastbedingungen, Randbedingungen usw.)
- Zielfunktion
- Einschränkungen
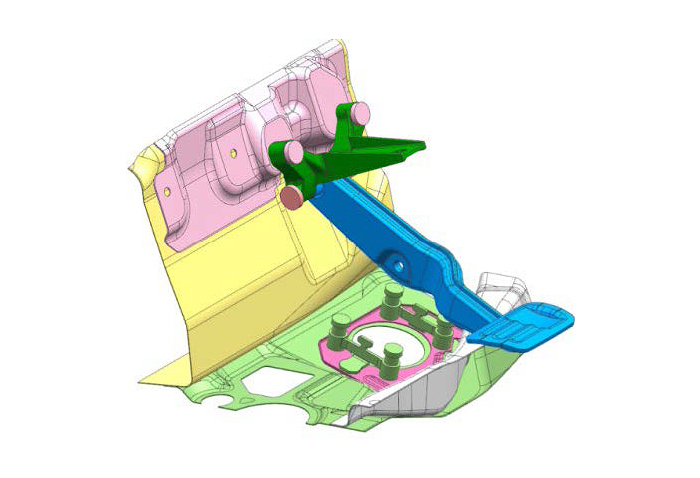
Der erste Konstruktionsraum ist der Bereich, in dem das Material des zu optimierenden Teils platziert werden kann. Legen Sie den Bereich fest, in dem das Zielteil innerhalb von Konstruktionsbeschränkungen wie Interferenzen mit anderen Teilen platziert werden kann. Je größer dieser Bereich ist, desto mehr Freiheit haben Sie bei der optimalen Konstruktion. Es ist auch möglich, Bereiche, in denen Material als Vorgaben platziert werden muss, als Nicht-Konstruktionsräume zu definieren. Wenn Sie beispielsweise ein Teil mit einer Schraube befestigen möchten, können Sie den Bereich in der Nähe der Schraube, um die Form zu fixieren, als Nicht-Konstruktionsraum definieren.
Der zweite Typ von Eingabedaten sind Informationen zu den Teilekonstruktionsspezifikationen. Informationen, die für eine normale Strukturanalyse erforderlich sind, wie z. B. Materialeigenschaften (Elastizitätsmodul und Poissonzahl), Belastungsbedingungen und Randbedingungen, werden auch für die Topologieoptimierung benötigt.
Das dritte, was wir brauchen, ist eine Zielfunktion. Eine Zielfunktion drückt aus: „Was genau wollen wir optimal erreichen?“ Wenn wir beispielsweise das Gewicht eines Teils reduzieren möchten, wäre die Zielfunktion „Minimierung der Masse“.
Die vierte Nebenbedingung gibt an, unter welchen Nebenbedingungen die Zielfunktion optimal ist. Wenn beispielsweise die Zielfunktion die Minimierung der Masse ist und keine Nebenbedingungen vorliegen, lautet die Antwort: „Masse des Konstruktionsraums = 0“. Dies bedeutet nicht, dass die Form optimal ist. Wenn Sie Gewicht reduzieren und gleichzeitig eine bestimmte Steifigkeit beibehalten möchten, können Sie die Nebenbedingung „Verformungsbetrag bei Belastung innerhalb von XX mm“ festlegen, um die Verteilung der Materialdichte innerhalb dieser Nebenbedingung zu optimieren.
Die oben genannten Informationen sind die Mindestinformationen, die zur Durchführung einer Topologieoptimierung erforderlich sind.
Darüber hinaus müssen auch Einschränkungen hinsichtlich der Herstellungsmethode berücksichtigt werden, und einige Softwareprogramme können eine Topologieoptimierung mit diesen festgelegten Einschränkungen durchführen.
Die Vorbereitung der oben genannten Informationen ist ein wichtiger Schritt für eine erfolgreiche Topologieoptimierung, da eine ordnungsgemäße Einrichtung die optimale Genauigkeit verbessert und zu einem effizienten Design führt.
Topologieoptimierungsprozess
Sobald die oben genannten Informationen vorliegen, können Sie die Topologieoptimierung durchführen. Sobald die entsprechenden Einstellungen vorgenommen und der Auftrag übermittelt wurde, wird die optimale Berechnung auf dem Computer durchgeführt, und der Bediener muss nur noch auf optimale Ergebnisse warten.
Hier möchte ich kurz den Ablauf optimaler Berechnungen erläutern. Ein vereinfachter Ablauf der Topologieoptimierungsberechnungen ist in Abb. 3 dargestellt.
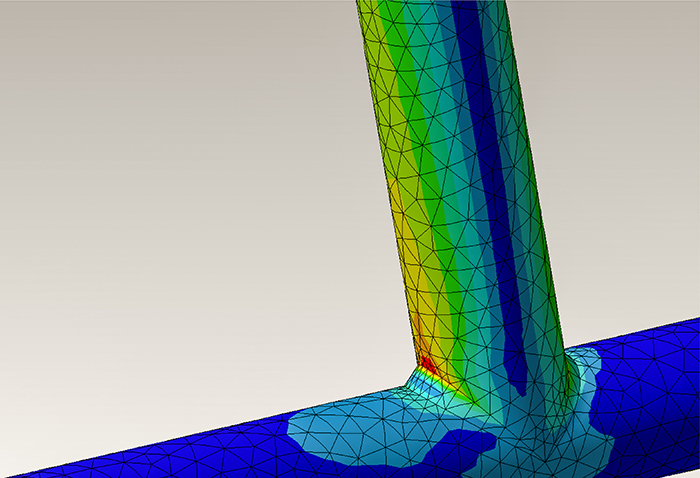
Für jede beliebige Form wird die Finite-Elemente-Methode (Strukturanalyse) angewendet, um die Zielfunktion und das Volumen zu berechnen. Erfüllt die Zielfunktion bestimmte Konvergenzbedingungen nicht, wird eine Sensitivitätsberechnung durchgeführt. Wir werden nicht näher auf die Sensitivitätsberechnung eingehen, aber es handelt sich um eine Berechnung zur Bestimmung der Richtung der Materialdichteverteilung. Die Materialverteilung im Entwurfsraum wird anschließend basierend auf den Ergebnissen dieser Berechnung aktualisiert, und eine numerische Berechnung mit der Finite-Elemente-Methode wird erneut durchgeführt. Sobald die Zielfunktion nach Durchlaufen dieser Schleife die Kriterien der Konvergenzbedingungen erfüllt, gilt die optimale Berechnung als abgeschlossen und die Berechnung endet.
Wenn Sie mehr über optimale Berechnungsmethoden erfahren möchten, schlagen Sie bitte in einem Fachbuch nach.
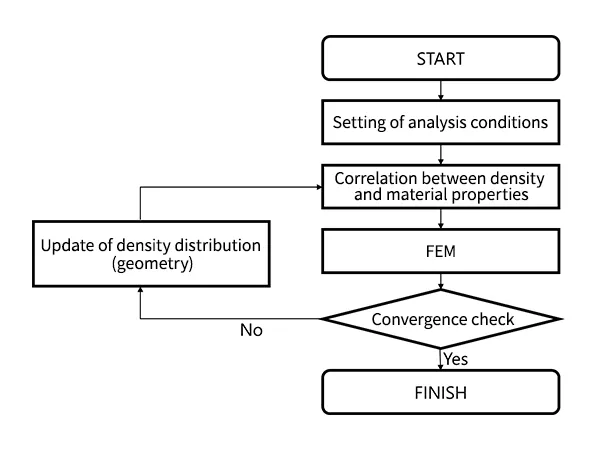 Abb. 3 Topologieoptimierungsprozess
Abb. 3 Topologieoptimierungsprozess
Teiledesign auf Grundlage der Ergebnisse der Topologieoptimierung
Die durch die Topologieoptimierung ermittelte optimale Form ist lediglich eine Extraktion der Materialdichteverteilung im Entwurfsraum und kann daher nicht unverändert als Entwurfsform verwendet werden. Es ist notwendig, CAD-Daten basierend auf den Ergebnissen zu konvertieren oder zu erstellen.
Dies ist der schwierigste Prozess bei der Anwendung der Topologieoptimierung auf die Teilekonstruktion. Die einfache Konvertierung der topologieoptimierten Form in CAD führt oft zu einer Form, die nicht gefertigt werden kann. Anders ausgedrückt: Dieser Prozess erfordert nicht nur Kenntnisse in CAE und Topologieoptimierung, sondern auch in der tatsächlichen Herstellbarkeit.
[Beispiel für Topologieoptimierung in der Praxis]
Auf der folgenden technischen Informationsseite finden Sie praktische Beispiele für die Teilekonstruktion mithilfe der Topologieoptimierung.
Topologieoptimierung | Asahi Kasei Engineering Plastics
Herausforderungen der Teilekonstruktion mittels Topologieoptimierung
Darüber hinaus müssen vor der Implementierung der Topologieoptimierung in die Teilekonstruktion auch Herausforderungen bewältigt werden.
- Vorbereitung einer Umgebung für die Topologieoptimierung: Es ist notwendig, Software vorzubereiten, die eine Topologieoptimierung durchführen kann, sowie die zugehörige Hardware. Ein optimaler Prozess erfordert wiederholte numerische Berechnungen mithilfe der Methode der finiten Elemente, daher muss die Hardware in der Lage sein, dies auszuhalten.
- Kenntnisse zur Topologieoptimierung: Sie benötigen Kenntnisse, um die für die Topologieoptimierung erforderlichen Informationen wie im vorherigen Abschnitt beschrieben richtig einzurichten.
- Anwendung der Ergebnisse der Topologieoptimierung auf das Produktdesign: Wie im vorherigen Abschnitt erwähnt, erfordert dies auch Kenntnisse zur Herstellbarkeit, was die größte Herausforderung von allen darstellt.
Asahi Kasei verfügt über die erforderliche Umgebung und das erforderliche Wissen zur Durchführung einer Topologieoptimierung sowie über Kenntnisse im Spritzgießen von Funktionsharzen und ist daher in der Lage, mithilfe der Topologieoptimierung optimale Designs für Harzteile bereitzustellen.
Wenn Sie leichtere und stabilere Kunststoffteile entwickeln möchten, können Sie sich gerne an uns wenden.
Zusammenfassung
In diesem Dokument werden die grundlegenden Konzepte und Methoden der Topologieoptimierung vorgestellt. Diese Technologie ermöglicht die Entwicklung leichterer und stabilerer Strukturen durch die optimale Anordnung der Materialien im Konstruktionsraum.
Bei der Umsetzung ist es wichtig, Informationen wie die Definition des Designraums, Materialeigenschaften, Belastungsbedingungen, Randbedingungen, Zielfunktionen, Zwangsbedingungen usw. richtig festzulegen. Darüber hinaus müssen bei der Abbildung optimaler Ergebnisse im tatsächlichen Produktdesign auch praktische Aspekte wie Herstellbarkeit und Konvertierung in CAD-Daten berücksichtigt werden.
Wenn Sie diese Punkte berücksichtigen, können Sie mithilfe der Topologieoptimierung effektiv leistungsstärkere Teiledesigns erreichen.
Für weitere Informationen zu CAE kontaktieren Sie uns bitte.
CAE-Download-Folien