- ARRIBA
- Fundamentos de CAE
- Parte 12: Optimización de la topología para el diseño
Serie: Fundamentos del análisis CAE para el diseño de productos plásticos
Parte 12 Optimización de la topología para el diseño
La optimización topológica es una tecnología innovadora que acelera el proceso de diseño, elimina el desperdicio y obtiene formas óptimas. Este curso presenta los conceptos y métodos básicos de la optimización topológica para quienes aún no la han utilizado.
2025.05.07

Contenido
Introducción
Para muchos diseñadores, mejorar la funcionalidad y el rendimiento de un producto supone un gran reto, a la vez que se cumplen limitaciones como el coste y la viabilidad de fabricación. La optimización estructural es un método para resolver este problema.
Se dice que el concepto de diseño óptimo de estructuras existe desde la década de 1980., y después de que las teorías básicas fueron estudiadas en círculos académicos, se aplicó en la industria y el poder computacional de las computadoras mejoró, y en los últimos años ha llegado a ser utilizado en una amplia gama de campos industriales.
Métodos de optimización estructural
Hay tres métodos principales para optimizar una estructura: tamaño óptimo, forma óptima y optimización topológica.
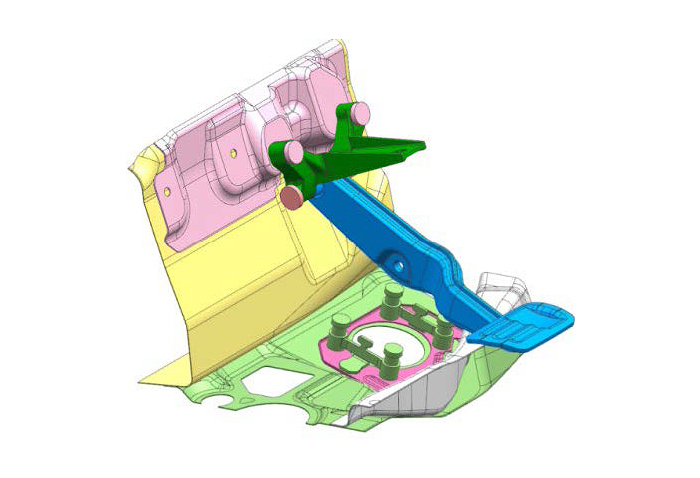
La dimensión óptima es una técnica para obtener dimensiones óptimas mediante el uso de dimensiones arbitrarias, como la longitud y el espesor de un componente, como variables, como se muestra en la figura 1(a).
La forma óptima es una técnica para optimizar la forma de una pieza utilizando la forma externa como variable, como se muestra en la Fig. 1(b).
Estas técnicas son adecuadas para ajustar la forma externa sin modificar la estructura básica. Sin embargo, no pueden modificar drásticamente la forma estructural, por lo que la estructura podría no ser óptima. Por lo tanto, la optimización topológica, que se muestra en la Fig. 1(c), es una técnica que permite optimizar con un mayor grado de libertad.
En este artículo, me gustaría presentar la optimización topológica, un tipo de óptimo estructural.
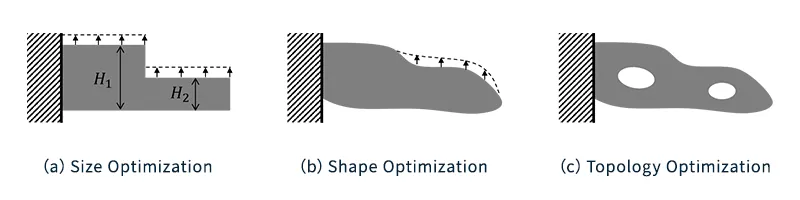 Fig. 1 Método estructural óptimo
Fig. 1 Método estructural óptimo
Características
La optimización topológica es un método estructural óptimo que calcula cómo organizar los materiales en el espacio que se va a diseñar para crear una estructura óptima.
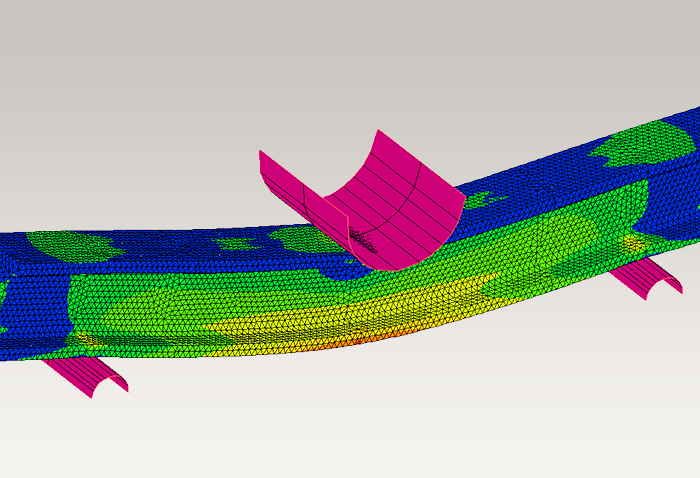
Por ejemplo, considere el caso donde ambos extremos están soportados y se aplica una carga a la superficie inferior, como se muestra a la izquierda en la Fig. 2. En la optimización topológica, el área en la que se pueden colocar los materiales, llamada espacio de diseño, en otras palabras, el rango para que sea óptimo, se divide en elementos pequeños y se realizan cálculos óptimos mientras se ajusta la densidad del material para cada elemento.
Un ejemplo de los resultados del análisis después de la optimización de la topología se muestra a la derecha en la Fig. 2. El color representa la densidad del material y, al colocar el material en las áreas de distribución de alta densidad que se muestran en rojo, es posible crear una estructura que garantice la resistencia de manera más eficiente.
La optimización topológica permite obtener una forma óptima con un grado tan alto de libertad que tiene la gran ventaja de poder derivar soluciones óptimas a las que sería difícil llegar utilizando únicamente la intuición humana.
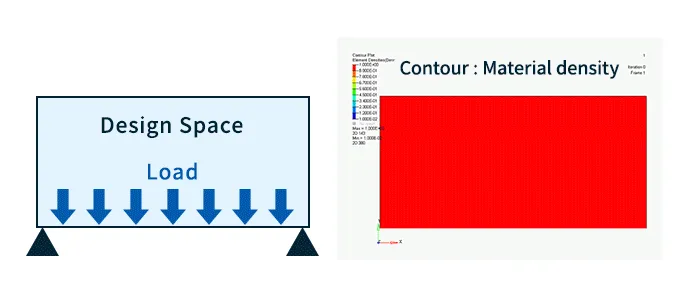 Fig. 2 Resultados de optimización topológica (Contorno: Densidad del material)
Fig. 2 Resultados de optimización topológica (Contorno: Densidad del material)
Información necesaria para la optimización de la topología
La optimización de la topología requiere la siguiente información:
- Espacio de diseño
- Varios datos de entrada (propiedades físicas, condiciones de carga, condiciones de contorno, etc.)
- Función objetivo
- Restricciones
El primer espacio de diseño es el área donde se puede colocar el material de la pieza que se desea optimizar. Establezca el área donde se puede colocar la pieza de diseño objetivo dentro de las restricciones de diseño, como la interferencia con otras piezas. Cuanto mayor sea esta área, mayor será la libertad para optimizar el diseño. También es posible definir áreas donde se debe colocar el material como espacios fuera de diseño. Por ejemplo, si desea sujetar una pieza con un perno, puede definir el área cerca del perno para fijar la forma como un espacio fuera de diseño.
El segundo tipo de datos de entrada es la información relacionada con las especificaciones de diseño de la pieza. La información necesaria para el análisis estructural normal, como las propiedades del material (módulo de Young y coeficiente de Poisson), las condiciones de carga y las condiciones de contorno, también es necesaria para la optimización topológica.
El tercer elemento que necesitamos es una función objetivo. Una función objetivo expresa "¿qué buscamos específicamente que sea óptimo?". Por ejemplo, si queremos reducir el peso de una pieza, la función objetivo sería "minimizar la masa".
La cuarta restricción indica bajo qué restricciones la función objetivo es óptima. Por ejemplo, si la función objetivo es minimizar la masa y no existen restricciones, la respuesta será "masa del espacio de diseño = 0". Esto no significa que la forma haya sido óptima. Si se desea reducir el peso manteniendo cierto nivel de rigidez, se puede establecer la restricción "la cantidad de deformación al aplicar la carga está dentro de XX mm" para optimizar la distribución de la densidad del material dentro de esa restricción.
Lo anterior es la información mínima necesaria para realizar la optimización de topología.
Además, también se deben tener en cuenta las restricciones del método de fabricación, y algunos programas pueden realizar la optimización de la topología con estas restricciones establecidas.
Preparar la información anterior es un paso clave para una optimización topológica exitosa, ya que configurarla correctamente mejorará la precisión óptima y dará como resultado un diseño eficiente.
Proceso de optimización de topología
Una vez preparada la información anterior, puede ejecutar la optimización topológica. Una vez completada la configuración y enviado el trabajo, se realizará el cálculo óptimo en la computadora y el operador solo tendrá que esperar los resultados óptimos.
Aquí, me gustaría explicar brevemente el flujo de los cálculos óptimos. La figura 3 muestra un flujo simplificado de los cálculos de optimización topológica.
Para cualquier forma, se utiliza el método de elementos finitos (análisis estructural) para calcular la función objetivo y el volumen. Si la función objetivo no cumple ciertas condiciones de convergencia, se realiza un cálculo de sensibilidad. No entraremos en detalles sobre el cálculo de sensibilidad, pero se trata de un cálculo para determinar la dirección de la distribución de la densidad del material. La distribución del material en el espacio de diseño se actualiza con base en los resultados de este cálculo, y se realiza un nuevo cálculo numérico mediante el método de elementos finitos. Tras este ciclo, una vez que la función objetivo cumple los criterios de convergencia, se considera que el cálculo es óptimo y finaliza.
Si desea saber más sobre los métodos de cálculo óptimos, consulte un libro especializado.
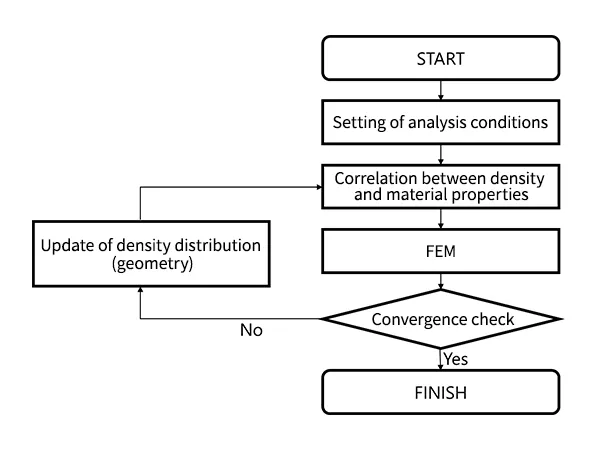 Fig. 3 Proceso de optimización de topología
Fig. 3 Proceso de optimización de topología
Diseño de piezas a partir de los resultados de optimización topológica
La forma óptima obtenida mediante la optimización topológica es simplemente una extracción de la distribución de densidad del material en el espacio de diseño, por lo que no puede utilizarse tal cual como forma de diseño. Es necesario convertir o crear datos CAD basados en los resultados.
Este es el proceso más difícil al aplicar la optimización topológica al diseño de piezas. La simple conversión de la forma optimizada a CAD suele resultar en una forma inmanufacturable. En otras palabras, este proceso requiere conocimientos no solo de CAE y optimización topológica, sino también de viabilidad de fabricación.
[Ejemplo de optimización topológica en la práctica]
Consulte la siguiente página de información técnica para obtener ejemplos prácticos de diseño de piezas utilizando optimización de topología.
Optimización topológica | Asahi Kasei Engineering Plastics
Desafíos del diseño de piezas mediante la optimización topológica
También existen desafíos que deben superarse antes de implementar la optimización topológica en el diseño de piezas.
- Preparación de un entorno para la optimización de topología: Es necesario preparar un software capaz de realizar la optimización de topología y el hardware asociado. El proceso óptimo requiere cálculos numéricos repetidos utilizando el método de elementos finitos, por lo que el hardware debe ser capaz de soportar esto.
- Conocimiento de optimización de topología: necesitará conocimientos para configurar correctamente la información requerida para la optimización de topología como se describe en la sección anterior.
- Aplicación de los resultados de optimización topológica al diseño de productos: como se mencionó en la sección anterior, esto también requiere conocimiento de capacidad de fabricación, que es el desafío más difícil de todos.
Asahi Kasei tiene el entorno y el conocimiento necesarios para realizar la optimización de topología, así como el conocimiento del moldeo por inyección de resinas funcionales y, por lo tanto, puede proporcionar diseños óptimos para piezas de resina utilizando la optimización de topología.
Si está buscando diseñar piezas de plástico que sean más ligeras y resistentes, no dude en contactarnos.
Resumen
Este artículo presenta los conceptos y métodos básicos de optimización topológica. La tecnología de optimización topológica que permite el diseño de estructuras más livianas y resistentes mediante la disposición óptima de los materiales en el espacio de diseño.
Al implementar esto, es importante configurar adecuadamente información como la definición del espacio de diseño, propiedades del material, condiciones de carga, condiciones de contorno, funciones objetivo, condiciones de restricción, etc. Además, al reflejar resultados óptimos en el diseño del producto real, también se debe prestar atención a cuestiones prácticas como la capacidad de fabricación y la conversión a datos CAD.
Teniendo en cuenta estos puntos, la optimización de la topología se puede utilizar de manera efectiva para lograr diseños de piezas de mayor rendimiento.
Para obtener más información sobre CAE, contáctenos.
Descargar diapositivas CAE