- TOP
- CAE解析の基礎知識
- 第1回 CAEとは -有限要素法(FEM)-
<連載>プラスチック製品設計のためのCAE解析基礎知識
第1回 CAEとは -有限要素法(FEM)-
CAEの基本知識と一般的に解析でよく使われる有限要素法(FEM)のポイントを紹介します。
目次
| 1. CAEとは |
| 2. CAEを最大限生かすために必要なもの |
| 3. 有限要素法(FEM)とは |
| 4. まとめ |
CAEとは
近年、CAE解析は機械設計を行う上で欠かせない技術となっています。CAE解析のCAE(シーエーイー)とは、Computer Aided Engineering の頭文字を取ったものであり、直訳すると「コンピューター支援設計」です。つまり、CAEとは 「製品設計、あるいはその前段階において、コンピューターを使ってその妥当性を検討するための手助けをする技術」 のことです。
製造業においてコンピューターが使用される以前は、形状や構造の細かい部分については、試作品を実際に作ってみなければ検証することができませんでした。いくつも試作品を作り、耐久性などの試験を経てからでなければ量産をスタートさせることができず、多くの時間とコストがかかっていたのです。
そのような状況の中アメリカでCAEが開発され、70年代には商用ソフトウェアが登場、80年代以降はコンピューターの能力の向上もあって大きく発展しました。設計開発の初期段階で数学的・物理的なモデルを作成し、コンピューターソフトウェアで目的とする製品仕様や性能、品質を予測し、製品設計の最適化を行います。
元々はロケットや飛行機などの金属材料の設計に使われ始めた技術ですが、現在ではプラスチック製品の開発にもなくてはならない技術になっています。この連載では、一般的なCAEの解説にとどまらず、プラスチックの特性上の違いや生産プロセスのシミュレーション、プラスチック製品の構造解析シミュレーションを解説します。
■ どうやって使うのか
製品設計や開発時に、CAEと共に使用されるのがCAD/CAMです。
CAD(キャド)とはComputer Aided Designの略で、設計業務を支援するシステムです。現在主として使用されている3D CADでは、2D CADではできなかった自由曲面の設計が可能となり、デザインの自由度が大きく向上しました。製造現場では、製品の3D CADデータを使用することで、そのまま金型の設計もCADで行うことができるようになりました。
CAM(キャム)とはComputer Aided Manufacturingの略で、NC工作機器を動かすためのデータの作成など、製品の生産に必要な情報を準備するシステムです。NC工作機械とは、コンピューターを使ったNumerical Control(数値制御)によって自動加工ができる工作機械のことです。従来は作業員が手作業でハンドルを回して切削などの加工を行っていましたが、NC工作機械に作業工程や寸法、位置などの切削条件を数値情報でプログラムすることで加工作業を自動化できます。
つまりCADで作成した設計データを、CAMで数値情報に変換することで、工作機械が自動で加工してくれるようになったのです。CADとCAMはソフトウェアが統合されていることが多いため、CAD/CAMとまとめて呼ぶこともあります。アナログ作業が大幅に削減されたことで、加工精度が向上し作業工程が効率化しました。
設計開発のフローとしては、CADを用いて製品や金型の設計を行い、CAE解析を行って製品製造上の問題を洗い出して設計データを修正し、CAMでNC工作機械へデータを送り、加工します。
CAEを用いることで、ものを作る前の、CADで作成した設計データの段階で評価を行うことができるようになりました。これまで試作品を作り、熟練技能者の経験や勘などによって行われてきた手直し・手戻り作業を、コンピューター上でシミュレーションすることで解析できるようになったのです。
■ CAEでできること
では、CAEではどのような解析を行うことができるのでしょうか。現在ではCAEの適用範囲は多岐にわたっており、それぞれ使用されるソフトウェアは異なっています。具体的には機械、電気/電子、建築、化学、医学などから、自然現象を解明することにも使用されており、私たちの生活に役立てられています。
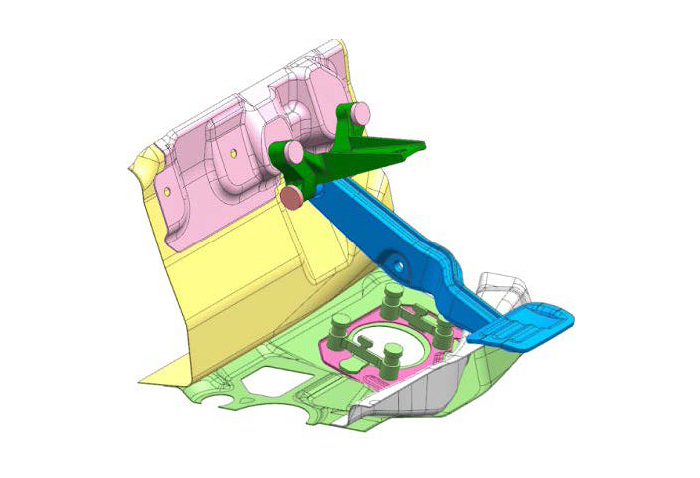
たとえば機械設計などでは、試作品を作らずとも製品の可動部がほかのパーツに干渉しないかなどを機構解析によって確認することができます。
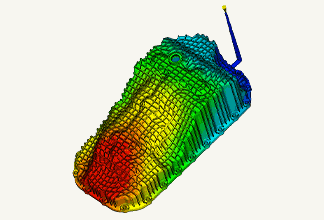
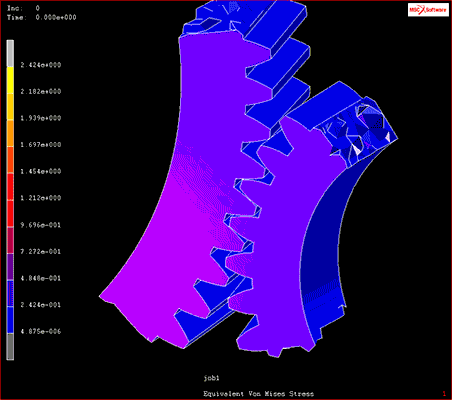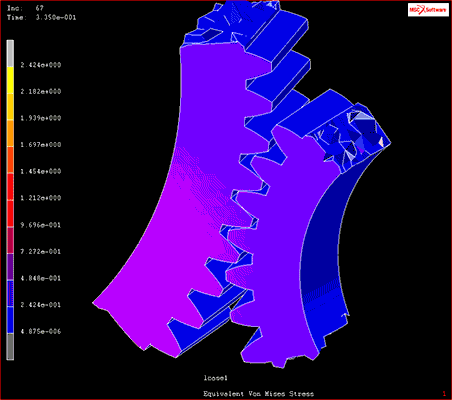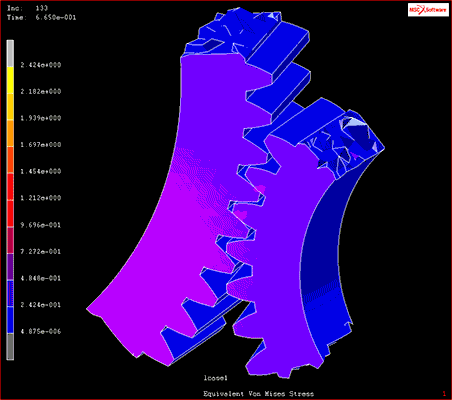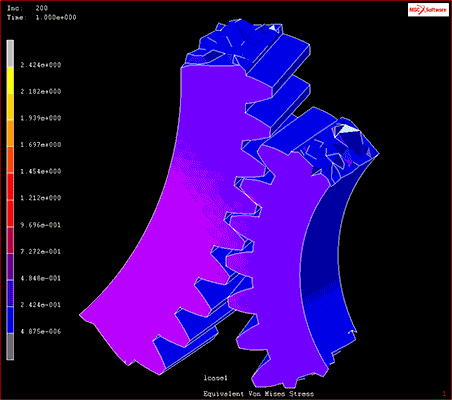 図1 機構解析の結果
図1 機構解析の結果
出典:MSC社「接触解析」・「破壊及び損傷解析」ムービー内のモデル(2021年2月26日)
*Model in the video of “Contact Analysis”, “Disruption and Damage Analysis”(Viewed February 26, 2021).
https://www.mscsoftware.com/product/marc
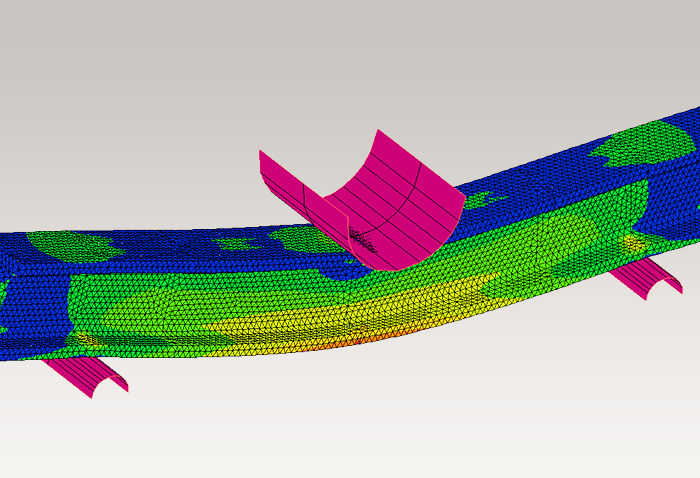
金型製作だけを取ってみても、プラスチック射出成形金型、鋳造型、ダイカスト型、プレス型などに使用されており、それぞれ適したソフトウェアが販売されています。プラスチック射出成形金型のCAE解析で一般的に使われているのは流動解析です。これによって、プラスチックを適切に金型に流し込めるかどうかをシミュレーションすることができるのです。
 図2 流動解析によって得られる樹脂の充填の様子
図2 流動解析によって得られる樹脂の充填の様子
■ 現代のものづくりには必須
CAEを用いてCADで作成した設計データの評価を行い、試作の回数を減らすことができるようになり、開発リードタイムの大幅な短縮、コストの削減が可能となりました。コンピューターの高性能化、低価格化とソフトウェアの進化によって、CADの作業中に設計者がCAEを利用することで、専門の技術者に解析を依頼するのではなく設計者自身が製品解析を行いながら設計することが可能になったのです。3D CAD/CAM、そしてCAEによって製造業のあり方が大きく変わったとも言えるでしょう。
現代では、開発期間の短縮化とコスト削減がますます求められており、CAE解析はこれからのものづくりにとって欠かせない技術と言えるのです。
CAEを最大限生かすために必要なもの
便利で有能なCAEですが、CAEを使いこなすにはソフトウェアだけでは不十分です。CAE解析結果は、何も知識を持たない人が見て、すぐに理解できるようなものではないためです。CAEの解析結果を正しく把握し、設計に反映させるためには、使用する解析ソフトウェアの使用方法だけでなく、材料力学といった工学的な基礎知識、そしてCAEの解析手法についての知識が必要となります。
■ 材料力学の基礎知識
材料力学とは、構造物に力が加わったとき、どのような力が作用して、変形したり壊れたりするのかということを知るための学問です。材料力学では、静止している構造物にかかる力は釣り合っていると定義し、力はベクトルで表されます。
構造物にかかる力を外力(荷重)といい、外力に抵抗する形で構造物の内部に生じる力を内力と呼びます。外力には、引張荷重、圧縮荷重、せん断荷重、曲げ荷重、ねじり荷重があります。この内力を評価するために使われるのが応力とひずみです。応力とは、単位面積あたりの内力と定義されます。
物体の内部にかかっている力は目に見えないので、物体を仮に切断したときの仮想断面の断面積や断面係数を用いて計算します。単位面積あたりで求めるのは、物体の大きさや太さに依存せず、単純に力の大きさを評価するためです。
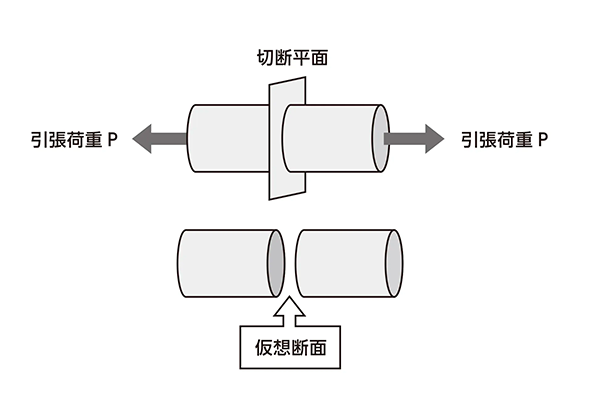 図3 応力を計算するために必要な仮想断面
図3 応力を計算するために必要な仮想断面
たとえば、丸棒を左右に引っ張る力、すなわち引張荷重Pを100 [N]とし、仮想断面の断面積を20 [mm2]とした場合、応力(σ)は以下の式で表されます。
応力σ=100/20=5 [N/mm2]
σ=100/20 N/mm2=5 N/mm2=5MPa
丸棒の内部に発生している応力は5 [N/mm2]ということになります。
ひずみとは、材料がどの程度変形したかということです。ひずみゲージを使って数値として測定することができるため、実機ではひずみを用いて評価することが多いのですが、設計では応力を用います。
材料力学では単純な構造であれば計算で求めることはできますが、実際の物体の構造は複雑なため、手計算で求めることは非常に困難です。たとえば、下図左のような構造の場合、材料力学を用いて応力を求めることは難しくありません。しかし、下図右のように、中に一つ穴を開けただけで、応力を求めることは非常に複雑になります。穴の周辺には応力が集中するためです。
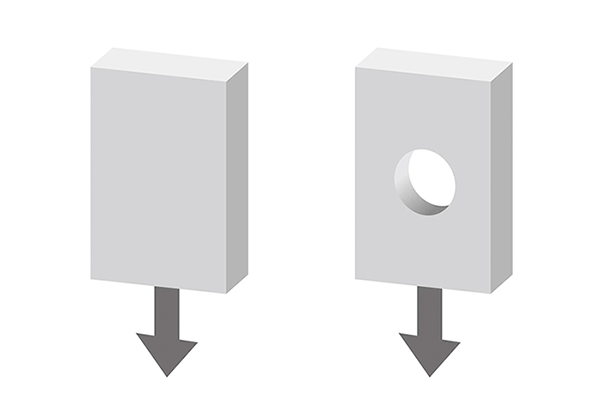 図4 手計算で容易に応力を求めることのできる例(左)とできない例(右)
図4 手計算で容易に応力を求めることのできる例(左)とできない例(右)
そこで利用するのが、CAE解析です。CAE解析を用いれば、複雑な形状でも容易に解析できます。
■ CAEの解析手法
CAEの解析では、物体の構造をさまざまな方法で分割して、解析しやすい形状にした上で、連立方程式を立てて近似解を求めるという手法をとります。方法としては主に、①有限差分法(FDM)、②境界要素法(BEM)、③有限要素法(FEM)の3つがあります。
①有限差分法(FDM:Finite Difference Method)は最も古くから使われてきた解析方法です。流れの解析によく用いられます。解析対象を差分格子と呼ばれる直交格子で分割して処理を行います。曲面で表現されたような複雑な境界条件では処理することが難しいという弱点があります。
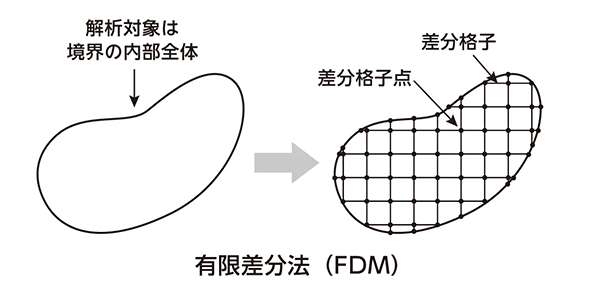 図5 有限差分法(FDM)
図5 有限差分法(FDM)
②境界要素法(BEM:Boundary Element Method)は領域の境界だけを解析する手法です。電磁場の解析によく利用されます。
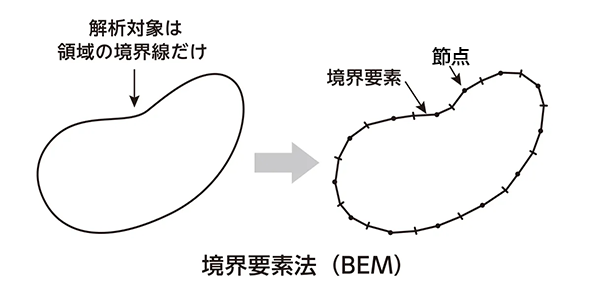 図6 境界要素法(BEM)
図6 境界要素法(BEM)
③有限要素法(FEM:Finite Element Method)は現在最も一般的に使用されている解析方法です。解析対象を三角形や四角形などに分割して解析します。2次元だけでなく、3次元解析にも対応しているため、構造解析、熱解析、応力解析、振動解析などを行うことができます。
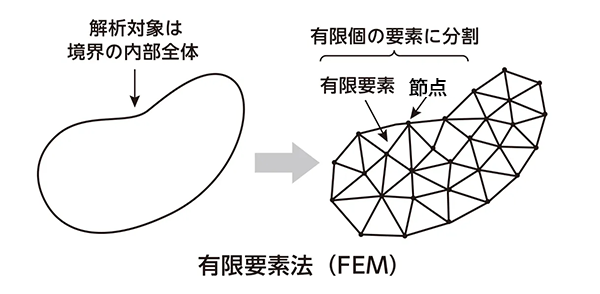 図7 有限要素法(FEM)
図7 有限要素法(FEM)
有限要素法についてさらに詳しく解説します。
有限要素法(FEM)とは
■ はじめは飛行機の構造設計
有限要素法は、1950年代に航空機の翼構造の強度解析を行うために実施されたのが始まりとされています。ジェットエンジンが実用化し、航空機の構造が複雑化したことによって、構造の強度計算を十分な精度で行うことが必要になったためです。
汎用デジタルコンピューターが利用されるようになった時代でもあり、コンピューターを利用することで、数値計算を高速で行うことができるようになりました。
■ 有限要素法の考え方
有限要素法では、解析対象の領域を三角形や四角形に細かく分割します。これをメッシュ(網)分割といいます。この分割された1部分を要素(Element)と呼び、要素を構成する頂点を節点(Node)と呼びます。
 図8 2次元モデルのメッシュ分割の例
図8 2次元モデルのメッシュ分割の例
3次元解析においては、立体形状(ソリッド)に分割することで解析を行うこともできます。
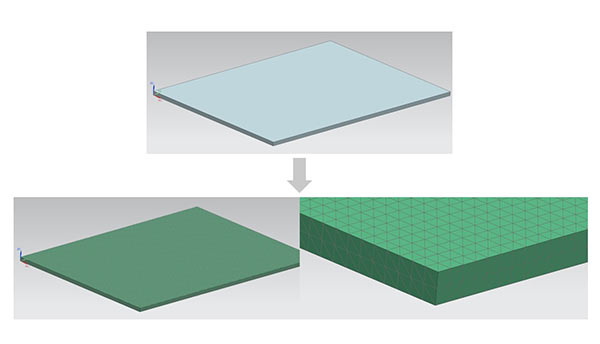 図9 3次元モデルのメッシュ分割の例
図9 3次元モデルのメッシュ分割の例
細かく分割した各要素について、かかる外力(重力や圧力など)から1次方程式を立てます。各要素は節点でつながっているため、1要素に作用した外力は節点を通して全体に伝達されると仮定します。そして要素ごとに得られる方程式をすべて合わせて連立1次方程式を立て、これを解くことで、各要素における変位や応力を求めることができます。つまり、複雑な問題を分割し、やさしい1次方程式にして解決する方法が有限要素法です。ただしこの連立1次方程式は、解析対象が複雑になると数千~数万という膨大な数になるため、マトリクスを用いたコンピューターによる演算が前提となります。
■ 有限要素法(FEM)のポイント
各要素の頂点に設置された節点を「1次要素」といいます。この節点は形状の中点などにも設ける場合があり、このような要素を「2次要素」と呼びます。
節点を増やすことによって、計算精度を向上させることができます。
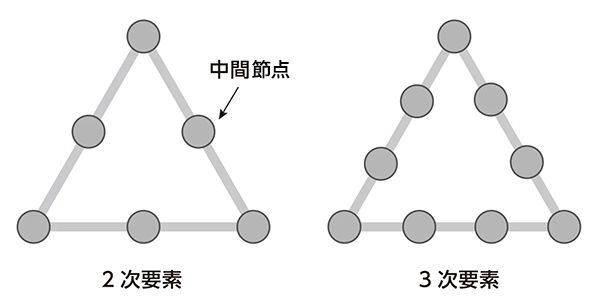 図10 要素の次数違いの例
図10 要素の次数違いの例
また、モデルを細かく分割し要素数を増やすことでも、より精度の高い解析ができます。すなわちより理論解に近づくということです。ただし、その分、計算時間は長くなってしまいます。一方で、どんなにモデルを細かく分割しても、現実の形状を完全に再現することはできません。CAE解析はあくまで、複雑な問題を計算しやすいモデルに変換することで近似値を求めるための手法なのです。
設計は限られた時間で行わなくてはなりません。また、これらの解析は開発リードタイムの短縮のために使用されているという側面があるため、どれだけの精度が必要か、解析の目的や状況に合った判断が求められます。
まとめ
3DCAD/CAMの導入、CAE解析によって、設計製造現場は大きく変容しました。現在では航空機や自動車に限らず、プラスチック製品など多くの分野で取り入れられています。これらの技術は、現在の製造業ではなくてはならないものとなっています。
とはいえ、ただコンピューターやソフトウェアを導入するだけでは、十分な効果を得ることはできません。CAE解析を活用するためには基礎的な原理、理論、知識を習得することが重要なのです。
次回は「プラスチックCAEのポイント -金属との違い-」についてご説明します。
◆最新回のリリース情報をメールで受け取ることができます。メールアドレスのみで登録できますのでご活用ください。メルマガ登録
CAEに関するお問いわせはこちらから